上 p(x=1) formula 299345-How do you calculate p(x)
Y 1 y 2 2 3The slope of the line through them, m = y 2 y 1 x 2 x 1 = rise run Lines can be represented in three di erent ways Standard Form ax by = c SlopeIntercept Form y = mx b PointSlope Form y y 1 = mX is a value that X can take;⇒λ = λ 2 / 10 ⇒λ = 10 Now, substitute λ = 10, in the formula, we get P (X =0 ) = (e – λ λ 0)/0

Recall That A Discrete Random Variable X Has Poisson Distribution With Parameter L If The Probability Homeworklib
How do you calculate p(x)
How do you calculate p(x)-= x(x1)(x2)1, and 0!Recall that for a PMF, \(f(x)=P(X=x)\) In other words, the PMF gives the probability our random variable is equal to a value, x We can also find the CDF using the PMF


2
List of common statistics formulas (equations) used in descriptive statistics, inferential statistics, and survey sampling Includes links to web pages that explain how to use the formulas, including sample problems with solutionsRecall that for a PMF, \(f(x)=P(X=x)\) In other words, the PMF gives the probability our random variable is equal to a value, x We can also find the CDF using the PMFPoisson Probability distribution Examples and Questions Poisson probability distribution is used in situations where events occur randomly and independently a number of times on average during an interval of time or space
1 1 Triola, Essentials of Statistics, Third Edition Copyright 08 Pea rson Education, Inc 53 Binomial Probability Distributions 2 Triola, Essentials ofOnce you have determined that an experiment is a binomial experiment, then you can apply either the formula or technology (like a TI calculator) to find any related probabilities In this lesson, we will work through an example using the TI /84 calculator If you aren't sure how to use this to find binomial probabilities,× (1/6) 3 (5/6) 1 = 4 × (1/6) 3 × (5/6) =
Calculator Use This online calculator is a quadratic equation solver that will solve a secondorder polynomial equation such as ax 2 bx c = 0 for x, where a ≠ 0, using the quadratic formula The calculator solution will show work using the quadratic formula to solve the entered equation for real and complex rootsThis formula returns "x" if the color in B5 is either "red" or "green", and the quantity in C5 is greater than 10 Otherwise, the formula returns an empty string ("") Explanation In the example shown, we want to "mark" or "flag" records where the color is either red OR green AND the quantity is greater than 10The binomial distribution for a random variable X with parameters n and p represents the sum of n independent variables Z which may assume the values 0 or 1 If the probability that each Z variable assumes the value 1 is equal to p, then the mean of each variable is equal to 1*p 0*(1p) = p, and the variance is equal to p(1p)


Geometric Distribution Wikipedia



Mean Of Random Variable Variance Of Random Variable
Find a formula for the probability distribution of the total number of heads obtained in four tossesof a balanced coin The samplespace, probabilities and the value of the random variable are given in table 1 From the table we can determine the probabilitiesas P(X =0) = 1 16,P(X =1) = 4 16,P(X =2) = 6 16,P(X =3) = 4 16,P(X =4) = 1 16 (1)Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutorPMF for discrete random variable X" " p_X(x)" " or " "p(x) Mean " "mu=EX=sum_x x*p(x) Variance " "sigma^2 = "Var"X=sum_x x^2*p(x) sum_x x*p(x)^2 The probability mass function (or pmf, for short) is a mapping, that takes all the possible discrete values a random variable could take on, and maps them to their probabilities Quick example if X is the result of a single dice roll


Aswarphysics Weebly Com Uploads 4 6 2 1 Advanced Level Mathematics Mechanics 1 Part4 Pdf


2
Y 1 y 2 2 3The slope of the line through them, m = y 2 y 1 x 2 x 1 = rise run Lines can be represented in three di erent ways Standard Form ax by = c SlopeIntercept Form y = mx b PointSlope Form y y 1 = mPrecalculus The Binomial Theorem The Binomial Theorem 1 Answer23 Solving x 2x1 = 0 by the Quadratic Formula According to the Quadratic Formula, x , the solution for Ax 2 BxC = 0 , where A, B and C are numbers, often called coefficients, is given by



Random Variable And Its Probability Distribution Ma Economics Karachi University


1
Or we could use the fact that X is a sum of n independent Bernoulli variables Because the Bernoulli variables have expectation p, EX = np Because they have variance p(1−pP(X = 2) P(X = 1) P(X = 0) binomcdf(12,03,4) ENTER ** To find P(X ≥ k) use binomcdf The function has three (3) arguments number of trials (n), probability of a success (p), number of successes (k) NOTE P(X > k) = 1 – binomcdf(n, p, k) and P(X ≥ k) = 1 – binomcdf(n, p, k–1)** Example 3 Let n = 12, p = 03 and k = 4 To findHow do you use the binomial formula to expand #(x1)^3#?



Binomial Distributions Complement Formula Video 3 Youtube



Binomial Distribution Formula Calculator Excel Template
Notice the different uses of X and x X is the Random Variable "The sum of the scores on the two dice";Once you have determined that an experiment is a binomial experiment, then you can apply either the formula or technology (like a TI calculator) to find any related probabilities In this lesson, we will work through an example using the TI /84 calculator If you aren't sure how to use this to find binomial probabilities,(1x)^1=1xx^2x^3__&__ up to infinity


Q Tbn And9gctnkywuz3wmxekkkozo31lo0inbbiadzvlrn9ebqube8v Voctx Usqp Cau



Solved I Show There Is A Unique Cubic Polynomial P X Fo Chegg Com
Continuous Random Variables can be either Discrete or Continuous Discrete Data can only take certain values (such as 1,2,3,4,5) Continuous Data can take any value within a range (such as a person's height)Let X be Binomial(n, p) The probability of having x successes in n trials is (where x!Putting this all together we have the probability of x H's in n tosses is P(X=x) = (n over x) p x (1p) (nx) This is a very brief explanation and should be done very slowly in class It is absolutely pointless to produce formulas without a valid explanation one would never know when to apply them


Binomial Distribution Formula Calculator Excel Template



Compute P X Using The Binomial Probability Formula Then Determine Whether The Normal Distribution Can Be Used Homeworklib
List of common statistics formulas (equations) used in descriptive statistics, inferential statistics, and survey sampling Includes links to web pages that explain how to use the formulas, including sample problems with solutionsPractice Binomial probability formula This is the currently selected item Practice Calculating binomial probability Next lesson Binomial mean and standard deviation formulasThe word 'trigonometry' being driven from the Greek words' 'trigon' and 'metron' and it means 'measuring the sides of a triangle' In this Chapter, we will generalize the concept and Cos 2X formula of one such trigonometric ratios namely cos 2X with other trigonometric ratios Let us start with our learning!



Formula For The Mean Of The Probability Distribution Docx Computing The Mean Of A Discrete Probability Distribution Lesson 3 Formula For The Mean Of Course Hero


Http Egyankosh Ac In Bitstream 1 Unit 3 Pdf
Compound Interest The future value (FV) of an investment of present value (PV) dollars earning interest at an annual rate of r compounded m times per year for a period of t years is FV = PV(1 r/m) mt or FV = PV(1 i) n where i = r/m is the interest per compounding period and n = mt is the number of compounding periodsThe formula says the probability of x successes in n trials is C(n,x) p^x (1p)^(nx) where C(n,x) means the number of combinations of n objects taken x at a time, p^x means p raised to the x power, and (1p)^(nx) means 1p raised to the nx powerThe formula for the distance d from a point P(x_1, y_1, z_1) to the line L Let P be a point not on the line L that passes through the point Q and R



How Do You Use The Binomial Probability Formula To Find The Probability Of X Successes Given The Probability P Of Success On A Single Trial For N 6 X 4 P 0 75 Socratic


4 Discrete Rand Vars
The formula says the probability of x successes in n trials is C(n,x) p^x (1p)^(nx) where C(n,x) means the number of combinations of n objects taken x at a time, p^x means p raised to the x power, and (1p)^(nx) means 1p raised to the nx powerP x(1−p)n − and that it's the sum of n independent Bernoulli variables with parameter p explicitly, which means using ugly tricks about the binomial formula;X − ky integer n ≥ 0 Binomial series X k α k!


Consider The Following Exponential Probability Den Chegg Com



Homework 3 Solution Write The Distribution For Formula And Determine Whether It Is A Probability Distribution Or Not If It Is Then Calculated Mean Variance Ppt Download
X − ky integer n ≥ 0 Binomial series X k α k!Xk = (1x)α x < 1 if α 6= integer n ≥ 0 2 Geometric sum= 1) E(X) = np = 3* 03 = 09 P(X=x)=!( )!!



Bernoulli Distribution Bernouli Distribution Programmer Sought


Solved Problem Statement The Binomial Distribution Consists Of The Probabilities Of Each Of The Possible Numbers Of Successes X On N Trials For Ind Course Hero
Notice the different uses of X and x X is the Random Variable "The sum of the scores on the two dice";1 1 Triola, Essentials of Statistics, Third Edition Copyright 08 Pea rson Education, Inc 53 Binomial Probability Distributions 2 Triola, Essentials ofFind P (X = 0) Solution For the Poisson distribution, the probability function is defined as P (X =x) = (e – λ λ x)/x!, where λ is a parameter Given that, P (x = 1) = (02) P (X = 2) (e – λ λ 1)/1!
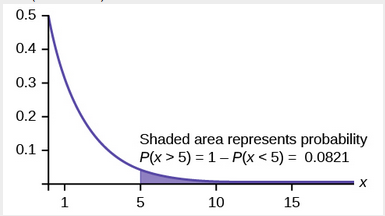


The Exponential Distribution Introduction To Statistics


Faculty Math Illinois Edu R Sowers Oldclasses 461stuff 461laugesens05 Pdf
λ = Σ f ⋅ x Σ f = 12 ⋅ 0 15 ⋅ 1 6 ⋅ 2 2 ⋅ 3 12 15 6 2 ≈ 094 The probability that he will score one goal in a match is given by the Poisson probability formula P (X = 1) = e − λ λ x x!= e − 094 094 1 1!Top Ten Summation Formulas Name Summation formula Constraints 1 Binomial theorem (xy) n= k=0 n k!



Pdf Formula Sheet Mohit Suhag Academia Edu
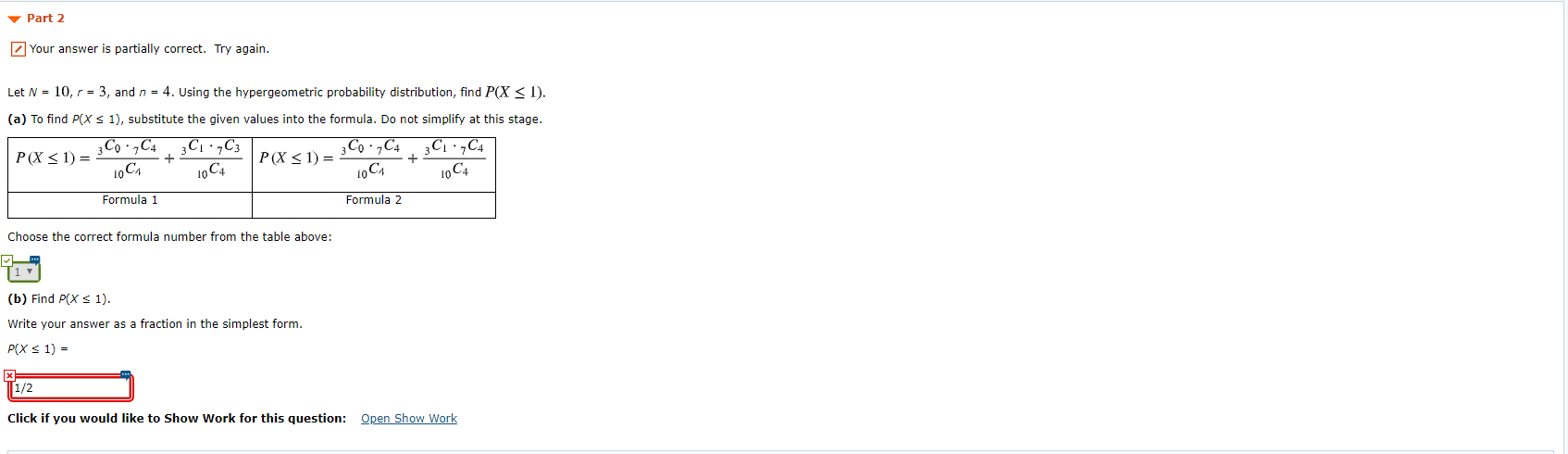


Solved Let N 10 R 3 And N 4 Using The Hypergeome Chegg Com
Continuous Random Variables can be either Discrete or Continuous Discrete Data can only take certain values (such as 1,2,3,4,5) Continuous Data can take any value within a range (such as a person's height)All equations of the form ax^{2}bxc=0 can be solved using the quadratic formula \frac{b±\sqrt{b^{2}4ac}}{2a} The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction1The distance between them, d(P;Q) = p (x 2 x 1)2 (y 2 y 1)2 2The coordinates of the midpoint between them, M = x 1 x 2 2;



Free Essays Homework Help Flashcards Research Papers Book Reports Term Papers History Science Politics


Http Www Utdallas Edu Nah1030 C sp18 Formulae C Pdf
Xk = (1x)α x < 1 if α 6= integer n ≥ 0 2 Geometric sumThe formula can be understood as follows k successes occur with probability p k and n − k failures occur with probability (1 − p) n − k However, the k successes can occur anywhere among the n trials, and there are ( n k ) {\displaystyle {\binom {n}{k}}} different ways of distributing k successes in a sequence of n trials1 A perfectly symmetric die that is equally likely to land on any of its 6 sides is thrown twice Let X be the upturned value of the first throw, and let Y be the sum of the two upturned values Find the joint probability mass function of X and Y 2 Seventy percent of the graduate students at the local university are domestic and thirty percent are international


Www Ualberta Ca Rjia Math418 Hwks Sol2 Pdf



Solved 1 The Probability Distribution Of A Discrete Rand Chegg Com
Then p = P(X = 1) = P(A) is the probability that the event A occurs For example, if you flip a coin once and let A = {coin lands heads}, then for X = I{A}, X = 1 if the coin lands heads, and X = 0 if it lands tails Because of this elementary and intuitive coinflipping example, a Bernoulli rv is sometimes referred to as a coin flipFormula P(x) = nCx (p)x (q)nx To calculate P(x) you need to know two things 1 how many combinations of outcomes would provide x number of successes, nCx 2 the probability of a success in any given trial (p) Calculating nCx The nCx looks kind of forbidding, but it's really just notation representing combinations (thus the capital C in theP(x = 1) = 4!1!3!


Http Www Utdallas Edu Nah1030 Stami Au19 Formulae Stam Pdf



Solved Let X Be A Random Variable With Pmf Px X X 2 A Chegg Com
× (1/6) 1 (5/6) 3 = 4 × (1/6) × (5/6) 3 = P(X = 2) = 4!= (02)(e – λ λ 2)/2!Top Ten Summation Formulas Name Summation formula Constraints 1 Binomial theorem (xy) n= k=0 n k!


Http Www Math Cmu Edu Users Weikang Math325 Solhw6 Pdf
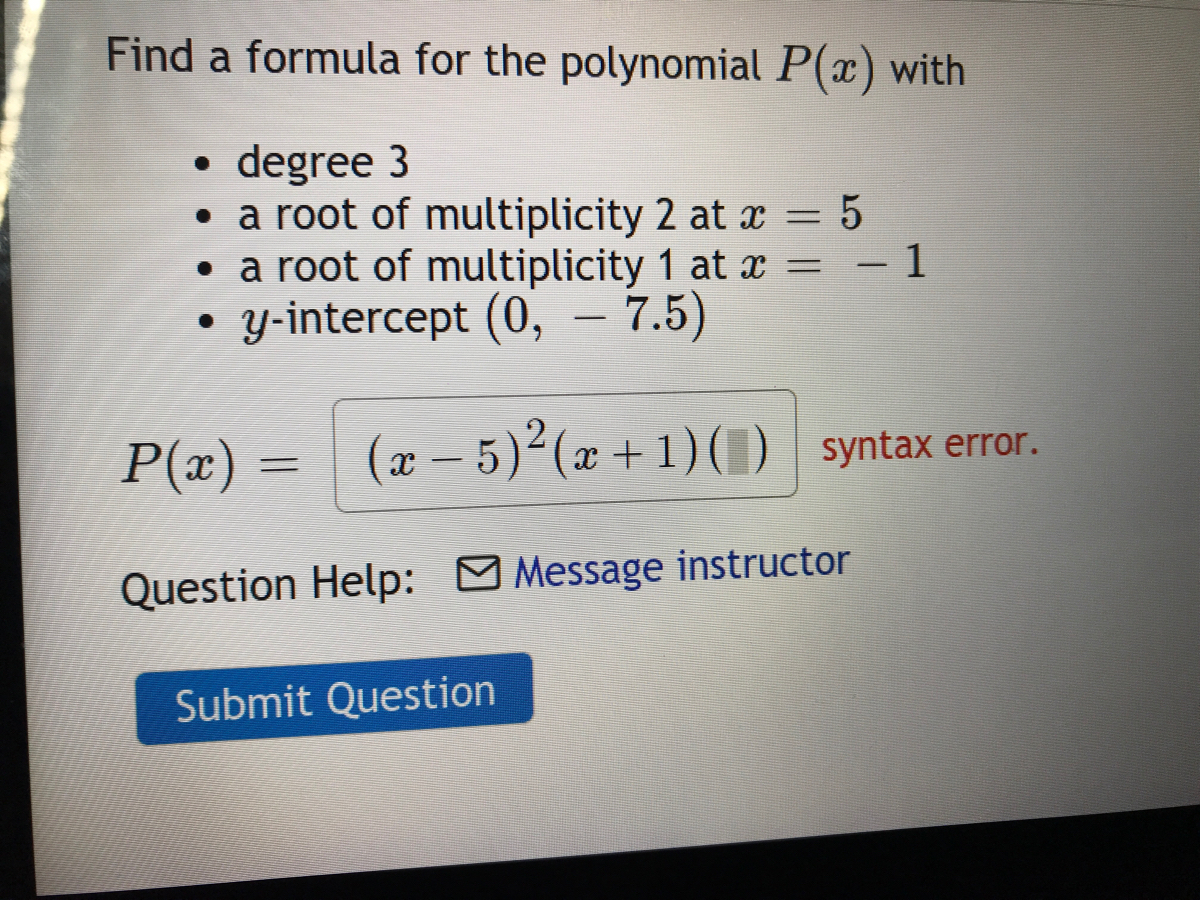


Answered Find A Formula For The Polynomial P X Bartleby
× (1/6) 2 (5/6) 2 = 6 × (1/6) 2 × (5/6) 2 = P(X = 3) = 4!Given that X is a Poisson random variable with {eq}\lambda {/eq} = 05, use the formula to determine the following probabilities a P(X = 0)You will need to pull out a common factor to write the sum in a form where the formula above is visibly applicable $\endgroup$ – Dilip Sarwate Oct 24 '13 at 141 Add a comment 2 Answers 2


2



Geometric Distribution Formula Calculator With Excel Template
X n x n − px (1p) nx VAR(X) = np(1p) = 3* 03 * 07 = 063 SD(X) = np(1p) Calculations shown for Binomial (n=3, p=03) = 0794 Note this is equivalent to counting success = 1 andP (15;10) = = 347% Hence, there is a 347% probability of that event to occur 15 times Example #2 Usage of the Poisson distribution equation can be visibly seen for improving productivity and operating efficiency of a firm1The distance between them, d(P;Q) = p (x 2 x 1)2 (y 2 y 1)2 2The coordinates of the midpoint between them, M = x 1 x 2 2;


Binomial Formula Explained
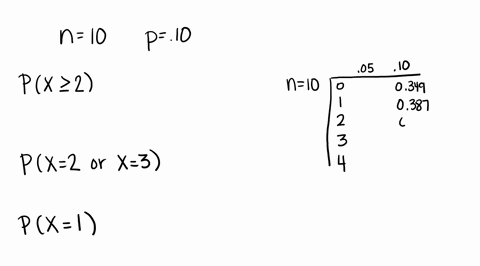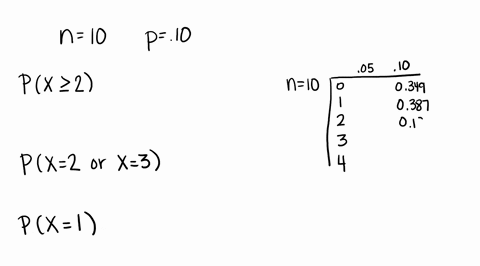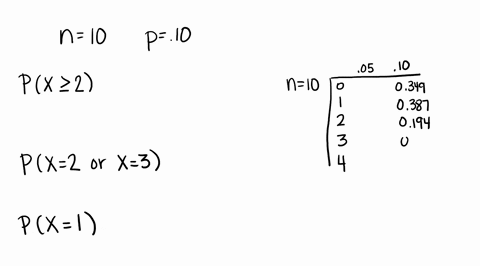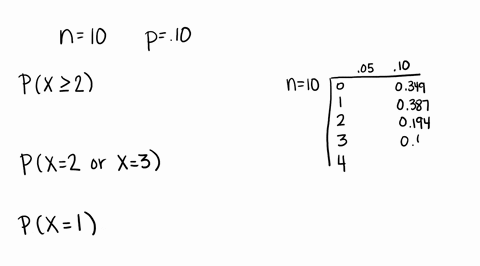


Solved Compute The Probability Of X Successes Us
X∞ (1−p)k As this last sum is a geometric series, and 1−p < 1, X∞ j=n P(X = n) = p 1 1−(1−p) = p 1 p = 1 The cumulative distribution function is given by P(X ≤ n) = 1−P(X > n) = 1− X∞ k=n1 (1−p)k−1p = 1− X∞ k=n (1−p)kp = 1−p (1−p)n p so P(X ≤ n) = 1−(1−p)n If X is a geometrically distributed randomYou will need to pull out a common factor to write the sum in a form where the formula above is visibly applicable $\endgroup$ – Dilip Sarwate Oct 24 '13 at 141 Add a comment 2 Answers 2You will need to pull out a common factor to write the sum in a form where the formula above is visibly applicable $\endgroup$ – Dilip Sarwate Oct 24 '13 at 141 Add a comment 2 Answers 2



Tree Representation Of Boolean Formula X 1 X 4 X 5 P 7 Download Scientific Diagram


View Question The Polynomial Of Degree 5 P X Has Leading Coefficient 1 Has Roots Of Multiplicity 2 At X 5 And X 0 And A Root Of Multiplicity 1 At X 5
X is a value that X can take;



Statistik 1 5 Distribusi Probabilitas Diskrit


Q Tbn And9gcrlhqgb0nmkf9opqbiv2phzg Ohrc0phczwr2pmbzcj0huiq0yh Usqp Cau



How To Calculate Probability Using The Poisson Distribution



The Binomial Distribution S Cool The Revision Website



Geometric Distribution Wikipedia



Solved Differential Equation Solve The Initial Value Xy Chegg Com



Solved 1 The Probability Distribution Of A Discrete Rand Chegg Com



Introduction To Probability Exponential Distribution Youtube
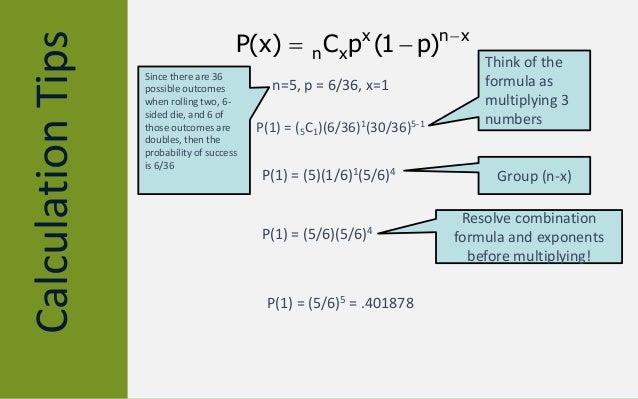


Binomial Probability Formula


Http Www Midwayisd Org Cms Lib Tx Centricity Domain 164 Ap stat 8 1a Pdf



Solved Find P X 3 To 4 Decimals Find P X Chegg Com
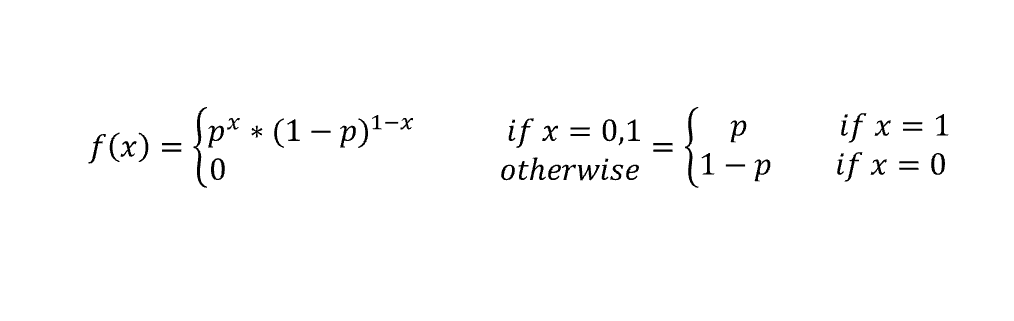


Understanding Bernoulli And Binomial Distributions By Valentina Alto Towards Data Science


A Factory Produces 5 Defective Items If A Sample Of 0 Items Is Taken At Random From The Production Find The Probability Of Getting More Than 4 Defective Items Quora


Http Faculty Weber Edu Mattondrus Oldcourses 2410 Docs Formulas Pdf


Faculty Math Illinois Edu Hildebr 370 408discrete1 Pdf
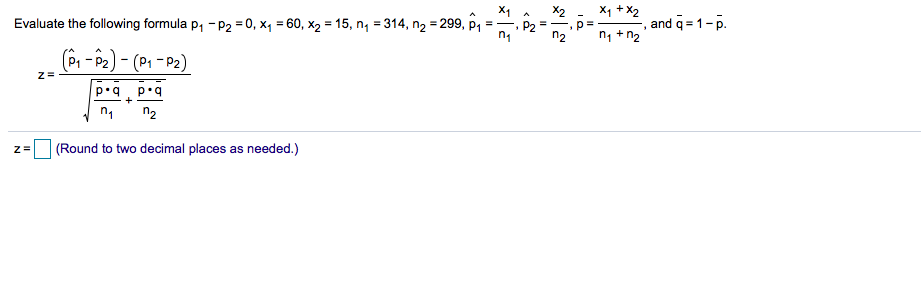


Answered X1 Evaluate The Following Formula P Bartleby


Http People Math Harvard Edu Knill Teaching Math464 1997 Math464 565 1997 Pdf



Answered Consider The Following Exponential Bartleby
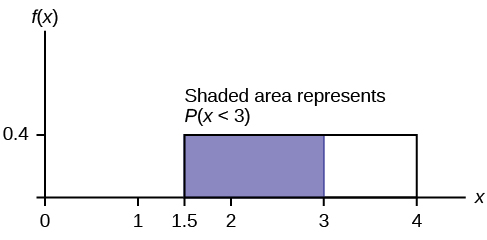


The Uniform Distribution Introduction To Statistics



Assignment04 Suppose That The Probability Distribution Of A Random



Chapter 6


Http Www Columbia Edu Ww40 6711f12 Homewk1sols Pdf


Interesting Application Of The Poisson Binomial Distribution Data Science Central



Probability Distributions Ppt Download



Answered Consider The Following Exponential Bartleby



Appendix Formulas Prepared For Dps5018 Exams Studocu


Www Jstor Org Stable



Ex 10 1 3 Find Distance Between P X1 Y1 Q X2 Y2 When


2


Http People Math Harvard Edu Knill Teaching Math464 1997 Math464 565 1997 Pdf


Http People Math Harvard Edu Knill Teaching Math464 1997 Math464 565 1997 Pdf



Finding Binomial Probabilities With A Formula Dummies



Overview Probability Distributions Ppt Download



How Do They Acquire This Cumulative Distribution Function Mathematics Stack Exchange



Binomial Probability Formula



The Indicated Function Y1 X Is A Solution Of The Given Differential Equation Use Reduction Of Order Brainly Com


Inst Eecs Berkeley Edu Cs1 Sp12 Slides Cs1 lecture 13 and 14 bayes nets representation and independence 2pp Pdf



From Artin Prove The General Formula Of Discriminant Of X N Px Q For N 2 Mathematics Stack Exchange
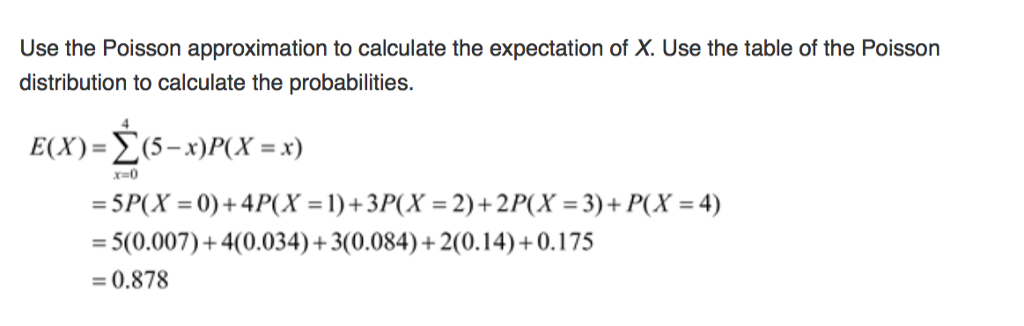


Solved How Was E X Formula Derived And How Were The Val Chegg Com



If In A Table All Possible Values Of A Random Variable Are Given Their Corresponding Probabilities Then This Table Is Called As



Recall That A Discrete Random Variable X Has Poisson Distribution With Parameter L If The Probability Homeworklib



Binomial Distribution Formula Step By Step Calculation Example



Binomial Distributions Cumulative Distribution Formula Video 2 Youtube



The Math P X 5 Pdf Free Download



Probability Distribution Formula Examples With Excel Template



Joint Cumulative Distributive Function Marginal Pmf Cdf



How To Find P X When You Are Given The Cdf Cumulative Distributive Function Hd Youtube



Discrete Random Variables The Binomial Distribution Bernoulli S



Solved X And Y Has A Joint Distribution Function Given By Chegg Com



Chap04 Discrete Random Variables And Probability Distribution
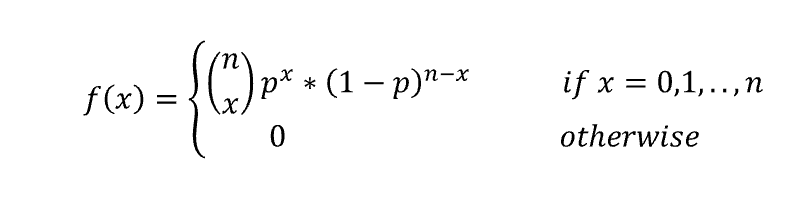


Understanding Bernoulli And Binomial Distributions By Valentina Alto Towards Data Science


2
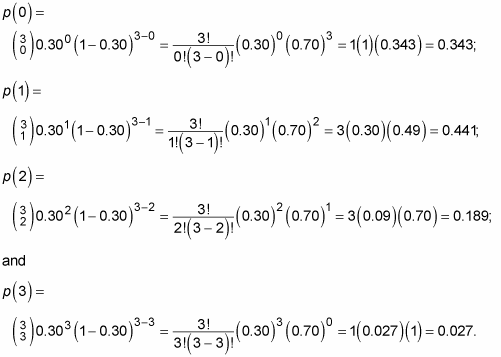


How To Find Binomial Probabilities Using A Statistical Formula Dummies



How To Compute The Probabilities Of Discrete Distribution Mathematics Stack Exchange



1 Binomial Random Variables Lecture 5 Many Experiments Are Like Tossing A Coin A Fixed Number Of Times And Recording The Up Face The Two Possible Ppt Download


Binomial Random Variables Biostatistics College Of Public Health And Health Professions University Of Florida



Computing Binomial Probabilities Youtube



Solved Consider The Following Exponential Probability Den Chegg Com



Discrete Random Variable An Overview Sciencedirect Topics



The Math P X 5 Pdf Free Download


Faculty Math Illinois Edu Hildebr 461 Exam3sol Pdf



Solved Possibly Useful Formulas Binomial P X Nx Px 1 Chegg Com



Ssf1063 Statistics For Social Sciences Lu5 Probability Distribution Of Discrete Random Variables 18 Th February Ppt Download
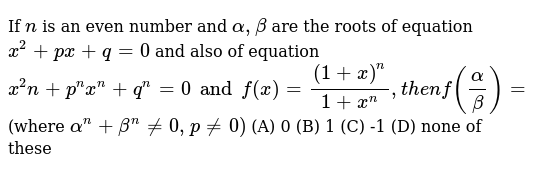


If X Is A Binomial Random Variable Compute P X For Each Of The


Q Tbn And9gcqzkjr5fprq Yb2jpocdojhtbmvrycundc7xg13lygc1ofovy0p Usqp Cau



Formual Sheet 16 Summary Quantitative Methods Of Economics 1 Studocu


コメント
コメントを投稿